Ricerca binaria: come trovare un numero tra 1 e 1 milione in 20 tentativi

• Python
• Howto

La creazione e l’ottimizzazione degli algoritmi di ricerca è uno dei problemi con i quali gli sviluppatori si sono da sempre misurati in campo informatico: l’ordinamento degli elementi che compongono un certo insieme è infatti una delle attività più costose dal punto di visto dell’impegno di tempo e di risorse macchina.

Si chiama ricerca binaria (binary search in inglese) quell’algoritmo che permette di individuare ciò che si sta cercando in un elenco ordinato di elementi.
La ricerca binaria cerca di risolvere il problema che ci si è posti suddividendo più volte a metà l’insieme degli elementi oggetto di verifica fintanto che le possibilità di scelta non vengono ridotte a una soltanto.

Per fare un esempio concreto e di immediata comprensione si supponga di voler indovinare a quale numero compreso tra 1 e 15 un’altra persona sta pensando. Si hanno al massimo 5 tentativi per vincere la sfida.
Impossibile usare un approccio randomico: le probabilità di perdere sarebbero però troppo elevate. Come fare, allora, per uscire sempre vincitori?

Usando la ricerca binaria si può suddividere l’insieme dei numeri da 1 a 15 in due ottenendo l’insieme tra 1 e 7 e tra 8 e 15. Come unico elemento si deve sapere se la risposta corretta sta nella prima o nella seconda metà dell’insieme preso in esame.
Supponendo di aver scelto 10 come numero da indovinare, si potrà dividere l’insieme 8…15 in due (8…11 e 12…15). Dividendo poi 8…11 in due (8…9 e 10…11) si riuscirà a indovinare il numero giusto in appena 4 tentativi.

Lo stesso schema può essere utilizzato per superare brillantemente sfide che solo all’apparenza appaiono molto più complesse. Per calcolare il numero massimo di tentativi che risultano necessari per trovare il risultato corretto con una ricerca binaria basta applicare la formula seguente:

n° max. tentativi = log2(n+1)

A “n” va sostituita la lunghezza della lista ovvero il numero di elementi ordinati che essa contiene. Ecco quindi che con un massimo di appena 20 tentativi è possibile indovinare un numero scelto nell’insieme compreso tra 1 e 1 milione.

Il semplice script Python che si può trovare in questa pagina (va rinominato in bin_search.py) non fa altro che automatizzare l’operazione di ricerca binaria usando un approccio ricorsivo.
Viene dapprima generato un array contenente un milione di elementi (generati in modo pseudocasuale tra 1 e 1.000.000 con la funzione random.sample) che viene ordinato ricorrendo al metodo sort().
Con la riga numero = a[5000] si è scelto di indovinare il numero che sta alla posizione 5000: ovviamente il numero della posizione all’interno dell’array può essere modificato e scelto liberamente.
L’insieme viene ripetutamente suddiviso a metà utilizzando la funzione bin_search e un approccio ricorsivo fino ad individuare ciò che si sta cercando.

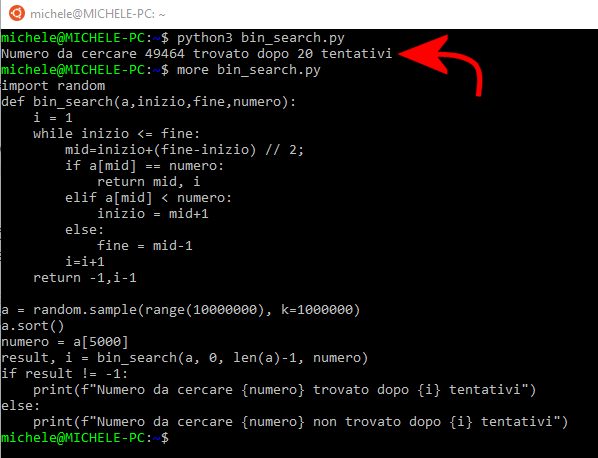
Eseguendo lo script Python (basta digitare python3 bin_search.py si otterrà una risposta del tipo “Numero N trovato dopo T tentativi“: come si vede, per un array formato da un milione di elementi, il numero massimo di tentativi richiesto risulta proprio pari a 20.

La “debolezza” dell’approccio presentato consiste proprio nella necessità, come più volte sottolineato, di ordinare i dati creando quindi un elenco ordinato. È questo uno dei problemi più rilevanti nel mondo informatico ma la ricerca binaria resta comunque un algoritmo efficiente che vale la pena di studiare.